Optimal transportation for ecological networks
Suppose you have a buffet with different desserts for a party. Given that the attendees have unique preferences, how do you determine the optimal partition of the desserts? I used this example in a blog post (and theory lecture) to explain the idea behind optimal transportation theory. Optimal transportation (OT) was initially developed for military logistics but is now a well-studied theory to manipulate probability distributions in machine learning and computer vision[1]. In our recent publication with Timothée Poisot, we take OT to ecology in a setting analogue to the dessert example. Given a population of bees and a field of flowers, which flowers will be visited by which bees? We can answer this question using OT!
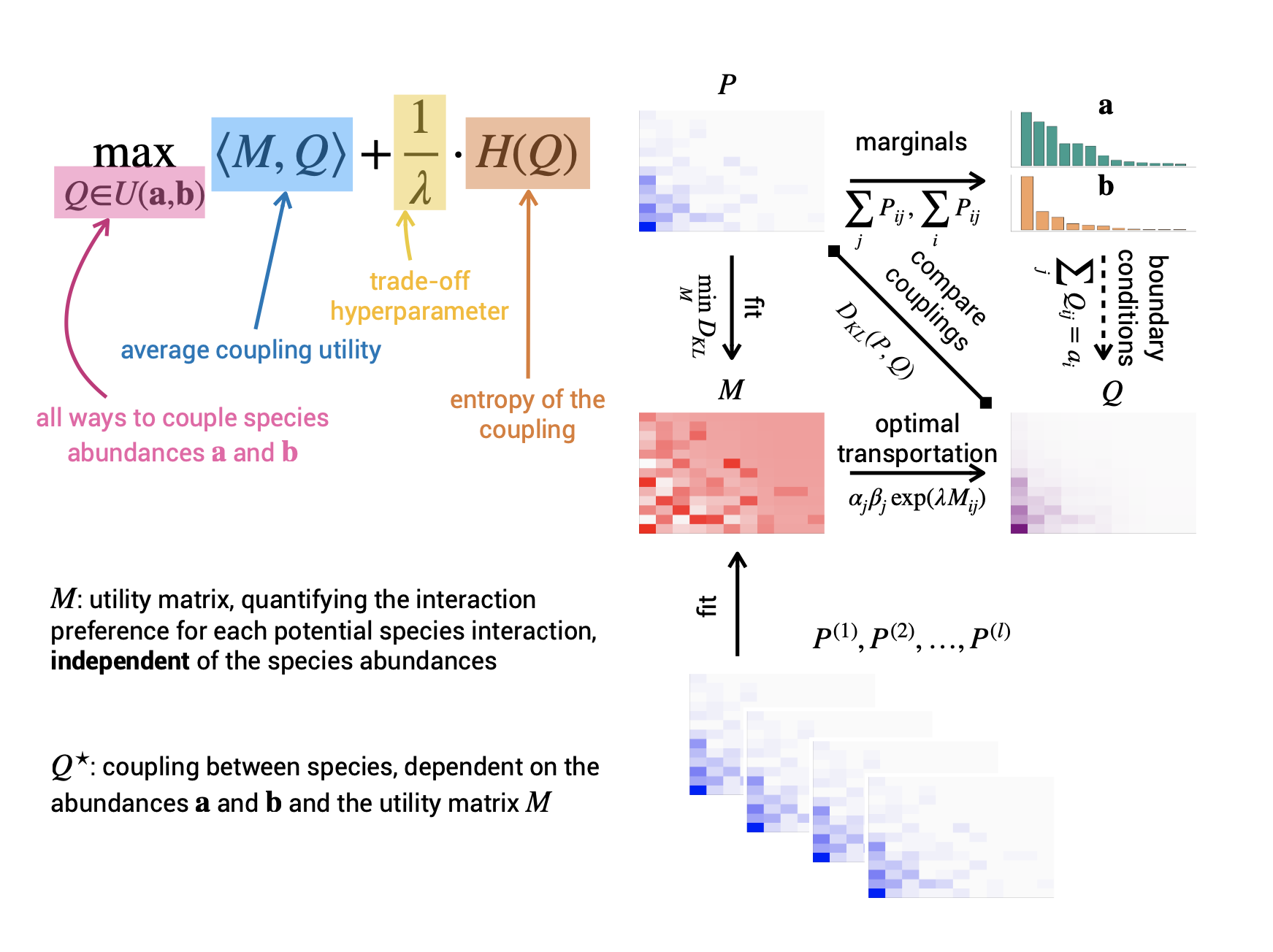
To find the ecological coupling between the bees and flowers (in general, between two trophic levels), we have to balance two forces. The first is the utility between bee species and plant species . Certain bees prefer certain species of plants (because of morphological comparability or because the plant's nectar has a suitable composition), so every bee species seeks to maximize utility. The second force is entropy, which drives the coupling to be as uniform as possible. The coupling that yields the optimal trade-off between these couplings can be obtained by solving an entropically-regularized OT problem. This optimization problem can be solved efficiently using the Sinkhorn algorithm.
The OT model is quite useful, as it decouples the abundances of the species from their preferences. The ecological coupling or interaction strength (e.g., frequencies of visits) arises as a consequence of both which species are present (and in which quantities) and their respective preferences. When two species compete for the given resource, one species can move to another less preferred resource. The nice thing about our framework is that it allows one to simulate how the interactions will change when the abundances change, think invasive species or extinction of some plant.
Maybe some ecologists are sceptical about how solving an optimization problem for the ecosystem might be justified. Are not all species only doing the optimal only for themselves and not the system? Well, our OT framework can be motivated as a maximum entropy (MaxEnt) model! Natural phenomena love to create entropy, and MaxEnt has been used successfully throughout the sciences (the Ideal Gas Law can be derived from it). Given two levels of species abundances and no preferences of one species for another, MaxEnt would predict the interaction strength between two species is proportional to their respective abundances. This so-called neutral model is already an excellent baseline in practice! The only addition to our model is that we add a linear functional of the interactions, saying that some are preferred over others[2]. In a sense, ours is the simplest possible Maxent model that uses information about interactions. We show that our OT solution arises naturally from species-level decisions, given that there is an element of randomness in the system.
Even though solving OT involves running a (simple) algorithm, it is still possible to compute a gradient at the utility matrix. If we do not know the utility matrix, we can estimate it from one or several observed interaction matrices! This allows for developing new statistical and machine learning models to find and predict interaction preferences, from which one can compute the interaction strength. For example, suppose you know traits or have phylogenetic distance between the species. In that case, you can fit a pairwise model to predict the utility (or abstraction of) for the species within the network. It is even possible to generalize to species outside the network, as we do in other work. From a technical point of view, the OT acts as just another link function.
M. Stock, T. Poisot and B. De Baets, Optimal transportation theory for species interaction networks
| [1] | For an excellent (technical) textbook on optimal transportation, see Computational Optimal Transport. |
| [2] | You can think about it as follows: if you apply the MaxEnt principle on a container of gas, assuming all molecules are the same, you would obtain that all molecules have the same concentration everywhere. Our model is similar to using some information on the molecules, for example giving them a weight and including gravity such that there is a higher pressure below. |