Scale: The Universal Laws of Growth, Innovation, Sustainability, and the Pace of Life in Organisms, Cities, Economies, and Companies
author: Geoffrey West
related books: Loonshots, Design in Nature, Cell Biology by the Numbers

The main take away
Organisma and organisations obey allometric laws of the form , which means that some property relates to the size/mass via a power-law. For living organisms, the exponent is often or . For example, metabolic rate (from mitochondria to whales) follows such a law closely (), as does the number of leaves on a tree () and the amount of sleep mammals need ().
These laws can be derived from the fractal nature of organisms. Living organisms consist of hierarchical organisation at different scales, e.g., molecules => membranes => organelles => cells => tissues => organs => bodies. If one assumes that these are evolved for optimal performance and that the smallest scales are fixed, one can derive the various scaling laws. The original paper of West derived these laws for circulatory (animals) and vascular (plants) systems. Living organisms are essentially four-dimensional due to their fractal composition.
Non-living organisations also following scaling laws. Properties of cities can accurately be predicted using the 15% rule on population size . Materialistic and infrastructure (such as the number of gas stations) increases sublinear . Social quantities (such as wages) rise superlinear . One can observe these laws in surprising ways; the larger a city, the greater the average walking speed. Interestingly, companies scale more similar to living beings, meaning that their productivity increases sublinear and they have a limited lifespan (compared to cities, which can last virtually forever).
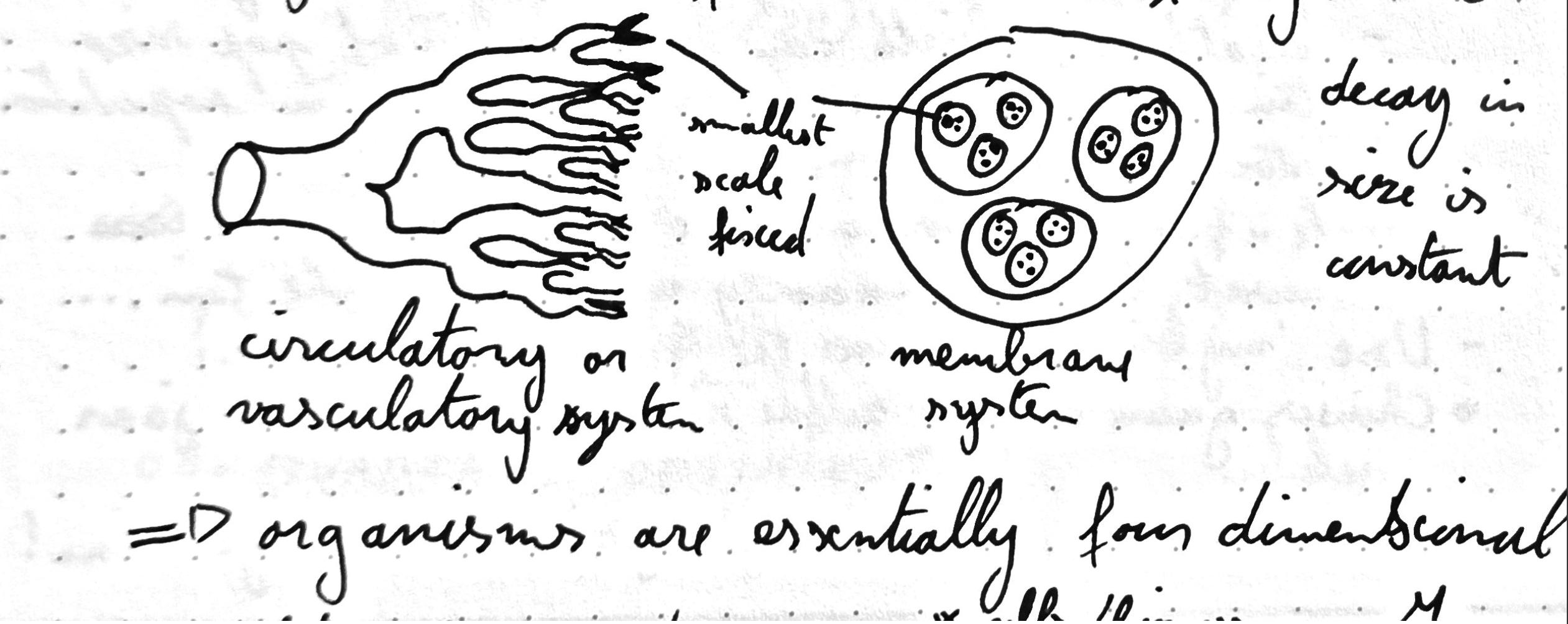
During my ecology and human nutrition courses, I was always fascinated by the allometric laws. However, it always confused me that the scaling power was 3/4 and not 2/3 (surface sphere divided by volume sphere). This book gave a satisfying answer to this puzzle (though I still had to read the original paper to grasp it entirely). As is often the case of these scaling laws, they are a good way to think about various processes but do not always fit the data unambiguously. One is advised to take the statements of this book with a grain of salt.
I also enjoyed reading a more technical paper that explores how the scaling laws impact evolution.
Who is this for?
You always had the glaring suspicion that biologists are too carried away into the details and that there is some simple principle that can explain nearly everything. You believe every scientific field is just physics applied.