Newton fractal in Julia using Symbolics.jl
The most recent video of 3blue1brown covered Newton fractals, a family of fractal curves that are obtained by applying Newton's method to complex numbers. Since I am covering Newton's method in my optimization course this week, it might be an entertaining illustration to play around with this topic.
Newton's method
Newton's method is a root-finding algorithm. We can use it to find roots of a function , i.e., inputs for which it holds that .
When executing Newton's method, we start with an initial and iteratively apply the following rule till convergence:
This rule can be derived by taking the first-order Taylor approximation of in and solving for the step that sets the approximation to zero.
Let us apply this to a simple function!
f(x) = x^3 - 1;For most functions, we can compute its derivative, and hence Newton update, easily enough. However, let us be lazy and use this opportunity to use Julia's new CAS Symbolics.jl. We write a function that takes a function as an input and computes the map above:
using Symbolics
function get_map(f)
# define variable
@variables x
# define derivative operator
Dx = Differential(x)
map = x - f(x) / Dx(f(x)) |> expand_derivatives
# now we expand and compile to a Julia function
update_expr = build_function(map, x)
return eval(update_expr)
end
update = get_map(f)#1 (generic function with 1 method)Yes! We get a new function: the update map! Let us try it on a value
update(2.0) # apply map once1.4166666666666665update(update(2.0)) # apply map twiceUndefVarError: update not defined
update(update(update(2.0))) # apply map thriceUndefVarError: update not defined
update(update(update(update(2.0)))) # apply map four timesUndefVarError: update not defined
We see that after a couple of steps, the Newton method converges to the root .
For our convenience, let us define a function that applies this map times.
function applyiteratively(x, update; n=100)
for i in 1:n
x = update(x)
end
return x
end
applyiteratively(2.0, update) # apply 100 timesUndefVarError: update not defined
Complex roots
Astute readers might have noticed that has three roots: one real () and two complex ones ( and ). Would our method also work with complex inputs?
applyiteratively(-2.0 - 2.0im, update)UndefVarError: update not defined
We see that this converges to a different (complex) root! Other values might converge to different roots!
applyiteratively(2.0 + 2.0im, update)UndefVarError: update not defined
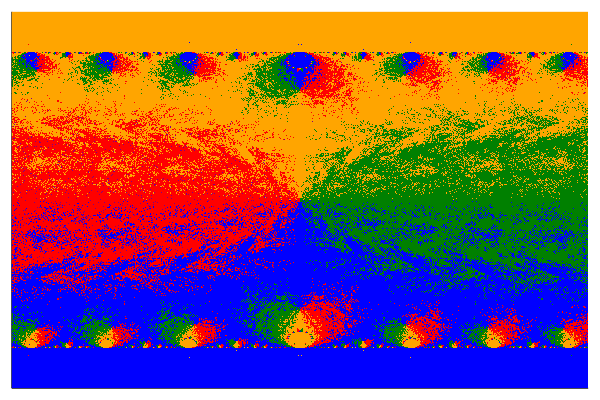
The Newton fractal
Imagine that we try this process for many complex numbers in an interval. Depending on the initial starting input, we end up in a different root. By colouring the results according to the root we end up in, we obtain the Newton fractal.
lower = -2 - 2im
upper = 2 + 2im
step = 0.5e-2
# generate a range of complex values
Z0 = [a+b*im for b in real(lower):step:real(upper),
a in imag(lower):step:imag(upper)]
# apply the update 100 times
Z100 = applyiteratively.(Z0, update);UndefVarError: update not defined
This results in a large complex matrix. We might define a colourmap for complex numbers as done here, though plotting the angle of the complex number in polar coordinates suffices.
using Plots
heatmap(angle.(Z100), colorbar=false, color=:rainbow, ticks=false)Failed to precompile Plots [91a5bcdd-55d7-5caf-9e0b-520d859cae80] to /home/runner/.julia/compiled/v1.7/Plots/jl_PdR1Cn.

Below are some other examples.
UndefVarError: get_map not defined

UndefVarError: get_map not defined